ktap Examples
These are some example one-liners and scripts for ktap: a script-based dynamic tracing tool for Linux. This is not an official ktap page, but rather my own collection of tools I'm using. These examples were written on Ubuntu precise (12.04.2 LTS).
Note: The ktap project stalled pending kernel integration and eBPF support, and has so far not continued. This page was last updated in 2014 and may not be updated again, so I've moved it to my Crypt. See my eBPF page for new developments in Linux tracing.
WARNING: This is open source software for an in-development tool, which may not yet be safe for production use. Use at your own risk. I'm currently using this in my own lab environment, just like I do with other unstable Linux tracers.
There's not a lot to see here yet... These examples will stop working from time to time as ktap evolves. Check the examples that come with ktap, which are kept more up to date as the code changes.
One Liners
# List all probes:
ktap -le
# List syscall enter probes (or use grep):
ktap -le 'syscalls:sys_enter_*'
# Tracing connect() syscalls by process name:
ktap -e 'trace syscalls:sys_enter_connect { print("connect() by: ", execname); }'
# Tracing heap size changes via brk() syscall:
ktap -e 'trace syscalls:sys_enter_brk { printf("%s called %s", execname, argstr); }'
# Tracing process execution (if probe exists):
ktap -e 'trace sched:sched_process_exec { print("running: ", pid, execname); }'
# Syscall count by syscall:
ktap -e 'var s = {}; trace syscalls:sys_enter_* { s[probename] += 1 } trace_end { print_hist(s); }'
# Syscall count by syscall, with starting text:
ktap -e 'var s = {}; printf("Tracing... Ctrl-C to end.\n");
trace syscalls:sys_enter_* { s[probename] += 1 } trace_end { print_hist(s); }'
# Syscall count by program:
ktap -e 'var s = {}; trace syscalls:sys_enter_* { s[execname()] += 1 } trace_end { print_hist(s); }'
# read() syscall by requested size distribution:
ktap -e 'var s = {}; trace syscalls:sys_enter_read { s[arg4] += 1 } trace_end { print_hist(s); }'
# read() syscall by returned size distribution:
ktap -e 'var s = {}; trace syscalls:sys_exit_read { s[arg2] += 1 } trace_end { print_hist(s); }'
# Stack profiling at 100 Hz, unsorted (see ktap's stack_profile.kp):
ktap -e 'var s = {}; profile-10ms { s[stack()] += 1 }
trace_end { for (k, v in pairs(s)) { print(k, v, "\n"); } }'
# Dynamic tracing of tcp_sendmsg() with stack traces:
ktap -e 'var s = {}; trace probe:tcp_sendmsg { s[stack()] += 1 }
trace_end { for (k, v in pairs(s)) { print(k, v, "\n"); } }'
# Tracing process execution, with simple (-s) info (currently broken):
ktap -s sched:sched_process_exec
I've included an example that has some starting text, so that you know when tracing has began. Instead of this, you could run these one-liners with "-v", verbose mode, for a similar effect. ktap's startup is fairly fast, so this is less necessary than it is with other tracing tools.
Sample One-Liner Outputs
Tracing heap size changes via brk() syscall:
# ktap -e 'trace syscalls:sys_enter_brk { printf("%s called %s", execname, argstr); }'
Tracing... Hit Ctrl-C to end.
date called sys_brk(brk: 0)
date called sys_brk(brk: 0)
date called sys_brk(brk: 1fdc000)
postgres called sys_brk(brk: 269d000)
postgres called sys_brk(brk: 26ca000)
postgres called sys_brk(brk: 26eb000)
postgres called sys_brk(brk: 270f000)
postgres called sys_brk(brk: 2730000)
postgres called sys_brk(brk: 2752000)
postgres called sys_brk(brk: 2774000)
[...]
Tracing process execution (if probe exists):
# ktap -e 'trace sched:sched_process_exec { print("running: ", pid, execname); }'
running: 1271 man
running: 1279 preconv
running: 1280 tbl
running: 1282 pager
running: 1281 nroff
running: 1283 locale
running: 1284 groff
running: 1285 troff
running: 1286 grotty
[...]
Syscall by syscall name:
# ktap -e 'var s = {}; printf("Tracing... Ctrl-C to end.\n");
trace syscalls:sys_enter_* { s[probename] += 1 } trace_end { print_hist(s); }'
Tracing... Ctrl-C to end.
^C
value ------------- Distribution ------------- count
sys_enter_rt_sigprocmask |@@@@@@@@@ 260
sys_enter_rt_sigaction |@@@@@ 166
sys_enter_read |@@@ 107
sys_enter_times |@@ 80
sys_enter_select |@@ 74
sys_enter_ioctl |@@ 71
sys_enter_write |@@ 64
sys_enter_poll |@ 43
sys_enter_mmap |@ 32
sys_enter_close | 25
sys_enter_newstat | 25
sys_enter_newfstat | 16
sys_enter_open | 16
sys_enter_access | 16
sys_enter_mprotect | 13
sys_enter_statfs | 11
sys_enter_getegid | 8
sys_enter_munmap | 8
sys_enter_geteuid | 8
sys_enter_getuid | 8
... |
read() syscall by returned size distribution:
# ktap -e 'var s = {}; trace syscalls:sys_exit_read { s[arg2] += 1 } trace_end { print_hist(s); }'
^C
value ------------- Distribution ------------- count
-11 |@@@@@@@@@@@@@@@@@@@@@@@@ 50
18 |@@@@@@ 13
72 |@@ 6
1024 |@ 4
0 | 2
2 | 2
446 | 1
515 | 1
48 | 1
Scripts
syslatl.kp: syscall latency as a linear aggregation. This script can be edited to adjust the step size, which is 10 ms by default.
UPDATE: this is now part of ktap, under samples/syscalls/syslatl.kp.
# ./syslatl.kp
Tracing syscalls... Hit Ctrl-C to end.
^C
LAT(ms)+ COUNT
0 378
10 0
20 0
30 1
40 0
50 0
60 0
70 2
80 0
90 0
100 33
110 0
120 2
130 0
140 2
150 0
160 2
The script loops from zero latency to the maximum seen, printing the counts for each latency range. As ktap is in development, it's possible an easier way to achieve similar output will be added.
opensnoop.kp: trace open() syscalls and print basic details. Useful for debugging as it can quickly show which data files, log files, and config files are in use by an application.
# ./opensnoop.kp PID COMM FD ERR PATH 15313 ktap 5 0 /sys/kernel/debug/ktap/trace_pipe_15313 15315 ssh 3 0 /etc/nsswitch.conf 15315 ssh 3 0 /etc/ld.so.cache 15315 ssh 3 0 /lib/x86_64-linux-gnu/libnss_compat.so.2 15315 ssh 3 0 /lib/x86_64-linux-gnu/libnsl.so.1 15315 ssh 3 0 /etc/ld.so.cache 15315 ssh 3 0 /lib/x86_64-linux-gnu/libnss_nis.so.2 15315 ssh 3 0 /lib/x86_64-linux-gnu/libnss_files.so.2 15315 ssh 3 0 /etc/passwd 15315 ssh 3 0 /usr/lib/ssl/openssl.cnf 15315 ssh 0 2 /root/.ssh/config 15315 ssh 3 0 /etc/ssh/ssh_config 15315 ssh 3 0 /etc/ld.so.cache 848 irqbalance 3 0 /proc/stat 848 irqbalance 3 0 /proc/interrupts 848 irqbalance 4 0 /proc/irq/0/affinity_hint [...]
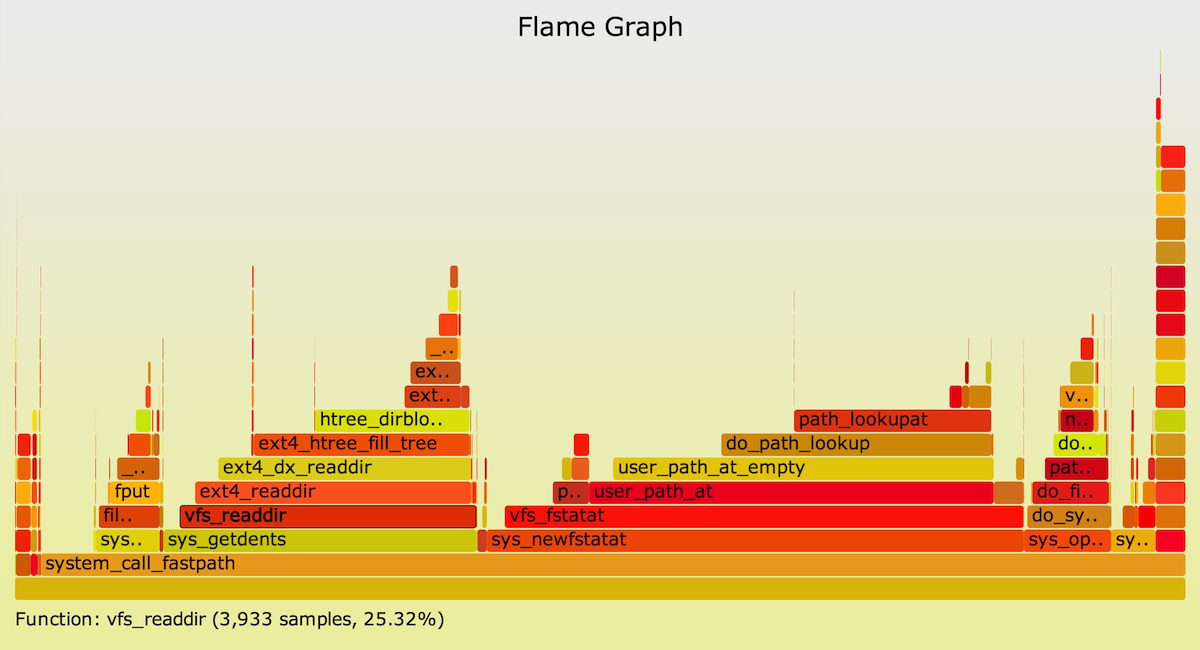
Flame Graphs
A Flame Graph visualizes stack traces, and ktap already supports their generation via the scripts/profiling/stack_profile.kp script. Here's an example using a ktap one-liner and the Flame Graph software:
# ktap -e 'var s = {}; profile-1ms { s[stack(100)] += 1 }
trace_end { for (k, v in pairs(s)) { print(k, v, "\n") } }
tick-30s { exit(0) }' -o out.kstacks
# sed 's/ //g' out.kstacks | stackcollapse.pl | flamegraph.pl > out.kstacks.svg
The sed(1) command remove tab characters (that's a tab, not a series of spaces), so that stackcollapse.pl can process the text. A stackcollapse-ktap.pl could be easily written to process ktap output directly, and avoid the need for sed(1).
The resulting flame graph:
Click for the interactive SVG, where you can mouse-over elements.
Setup
Last time I installed ktap on Ubuntu 13.10 (kernel: 3.11.0-17-generic), I used these steps:
apt-get install git gcc make libelf-dev git clone https://github.com/ktap/ktap cd ktap make make install make load
Took 5 minutes. As said earlier, this is still in development, so I'm only using it in lab environments at the moment.
Links
- www.ktap.org
- ktap tutorial from ktap.org
- ktap project on github
- ktap presentation (PDF) by Jovi Zhangwei at LinuxCon Japan, 2013